Giới thiệu
Kiểm định thống kê (test statistic) là một công cụ quan trọng trong thống kê giúp chúng ta đưa ra quyết định về tính chính xác của giả thuyết thống kê dựa trên dữ liệu mẫu. Vậy cụ thể kiểm định thống kê (test statistic) là gì? Có các loại kiểm định thông dụng nào? Hãy cùng FES tìm hiểu thông qua bài viết dưới đây nhé.
Kiểm định thống kê là gì?
Trong thống kê, kiểm định (tests) là các đại lượng cần tính khi chúng ta muốn kiểm tra một hoặc nhiều giả thuyết về dữ liệu thu thập được. Kiểm định thống kê được tính dựa trên các giá trị dữ liệu đã thu thập, và sau đó so sánh giá trị này với một giá trị tới hạn (critical value) để quyết định xem giả thiết không (H0) có bị bác bỏ hay không.
*Note: Giá trị tới hạn thường được xác định tùy theo các loại kiểm định và phân phối của chúng
Mỗi loại kiểm định sẽ sử dụng một công thức tính toán khác nhau và dựa vào phân phối dữ liệu mà chúng ta đang nghiên cứu.

Các loại kiểm định thông dụng và phân phối của chúng
Kiểm định Z (Z-test)
Kiểm định Z thường được sử dụng với kích thước mẫu lớn (>30) và khi biết được phương sai của tổng thể vì kiểm định này dựa trên phân phối chuẩn.
- Khi kích thước mẫu lớn (n>30), theo Lý thuyết Giới hạn Trung tâm (Central Limit Theorem), phân phối của giá trị trung bình mẫu sẽ xấp xỉ phân phối chuẩn.
- Kiểm định Z sử dụng độ lệch chuẩn của tổng thể trong công thức, vì vậy nó thường được sử dụng khi ta đã có thông tin của tổng thể, tránh việc gia tăng sai số trong kiểm định.
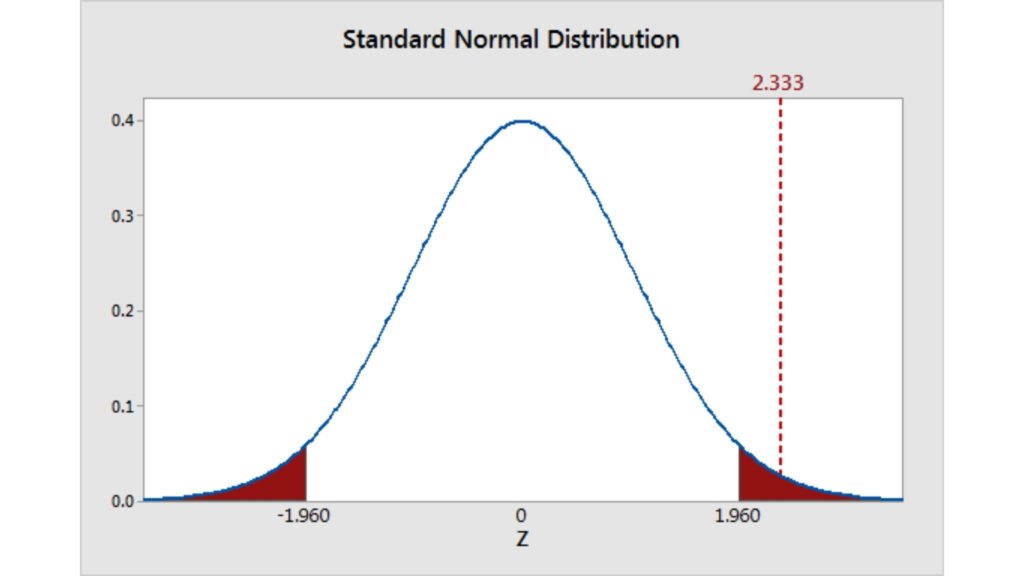
Kiểm định t (t-test)
Kiểm định t thường được sử dụng khi kích thước mẫu nhỏ hoặc khi không có thông tin về phương sai của tổng thể. Kiểm định này sử dụng phân phối t-Student, có dạng hình chuông giống phân phối chuẩn nhưng phần đuôi dài hơn.
Khi mẫu nhỏ và độ lệch chuẩn được ước tính từ mẫu thay vì từ tổng thể, độ chính xác của kiểm định Z giảm đi vì dữ liệu có thể có sai số và không tuân theo phân phối chuẩn. Phân phối t, với phần đuôi dài hơn, cho phép xử lý tốt hơn các sai số lớn trong trường hợp này.
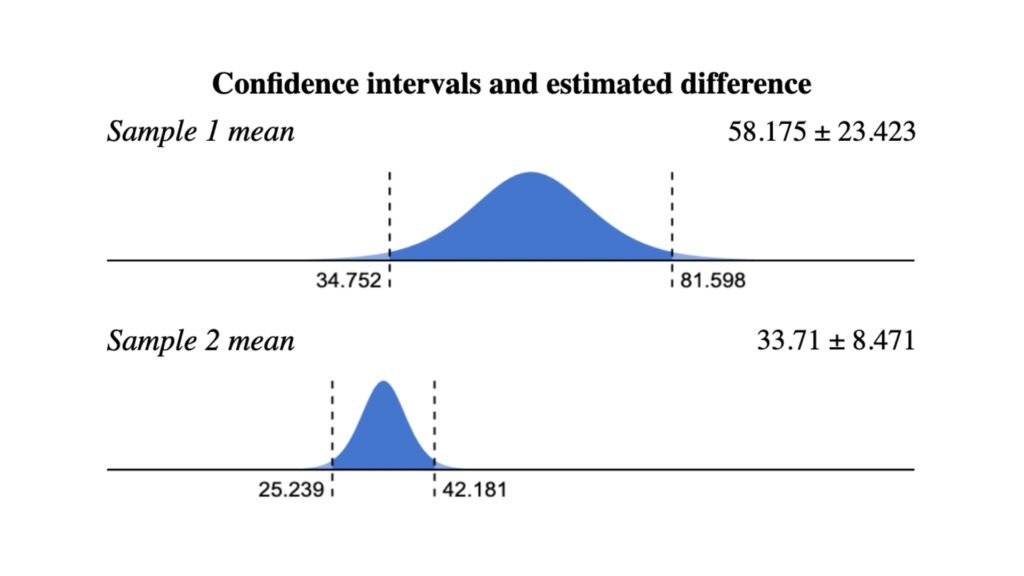
Kiểm định Chi-Bình phương (Chi-square test)
Kiểm định Chi-square chủ yếu được sử dụng để kiểm tra sự độc lập giữa hai biến phân loại hoặc kiểm tra sự phù hợp của một mẫu với phân phối lý thuyết. Kiểm định Chi-bình phương sử dụng phân phối Chi-square.
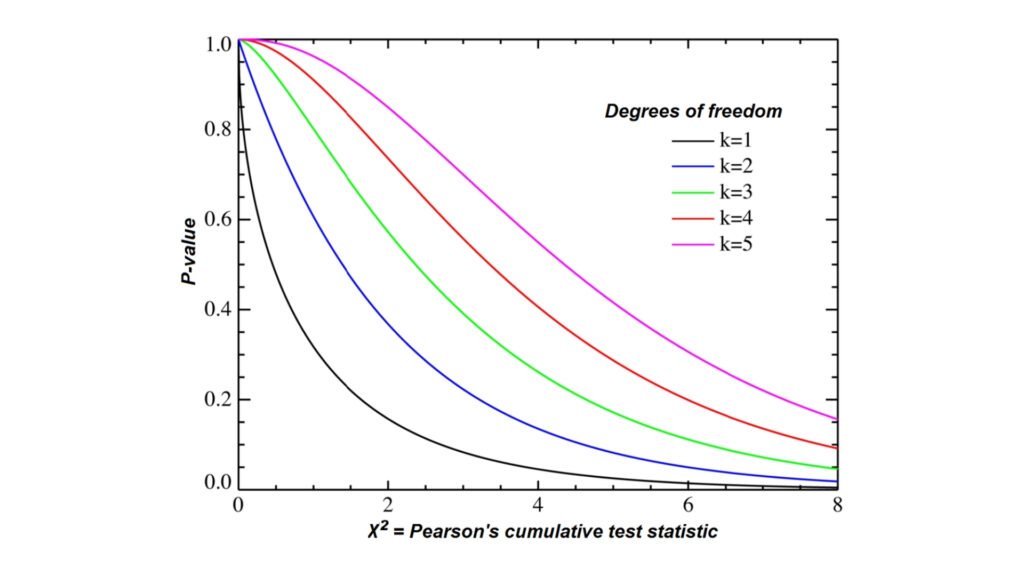
Kiểm định F (F-test)
Kiểm định F dùng để kiểm tra sự chênh lệch giữa phương sai của 2 mẫu. Kiểm định này sử dụng phân phối F.
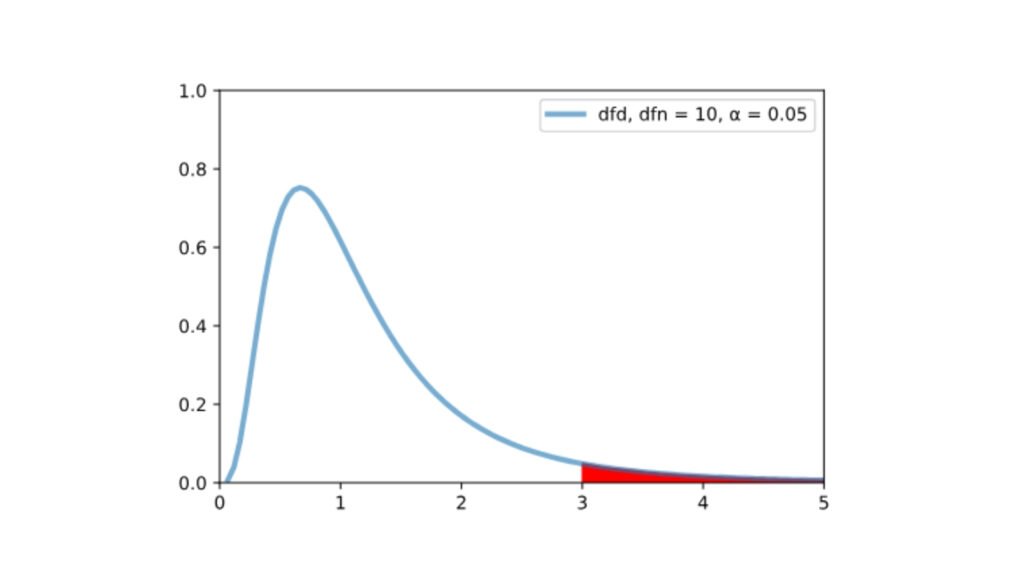
Bậc tự do
Bậc tự do là một khái niệm quan trọng trong các bài kiểm định thống kê. Nó xác định số lượng giá trị độc lập có thể thay đổi trong mẫu mà không làm thay đổi giá trị tính toán của kiểm định. Từng loại kiểm định khác nhau sẽ có bậc tự do đi kèm khác nhau.
Ứng dụng của các loại kiểm định
Mỗi loại kiểm định có đặc điểm riêng, vì vậy sẽ phù hợp với các mục đích khác nhau. Ứng dụng của các kiểm định trên được tóm tắt tóm tắt trong bảng sau:
Lời kết
Các kiểm định thống kê là công cụ quan trọng giúp chúng ta kiểm tra tính chính xác của giả thuyết dựa trên dữ liệu thu thập được. Mỗi loại kiểm định có ứng dụng riêng phù hợp với từng tình huống và mục tiêu nghiên cứu khác nhau. Việc hiểu và sử dụng đúng các kiểm định sẽ giúp đảm bảo độ chính xác và tin cậy trong phân tích dữ liệu, từ đó hỗ trợ ra quyết định trong các lĩnh vực nghiên cứu và ứng dụng thực tiễn.
Xem thêm các bài viết: Thông tin CFA, Tin tức thị trường, Tổng hợp công thức CFA, Đăng ký thi CFA


